|
|
Post by yardstick on Aug 2, 2017 21:29:09 GMT -6
So in response to an inquiry in another thread about 10th+ dimensional beings and our 'perfected bodies' after the Harpazo, I offered to make a Math Class thread, for purposes of demonstrating as many dimensions as I know how. I'll try to keep it in as plain english as I can. I expect this to be a very long thread so I appreciate your patience wading through a lot of math. I'll try to keep it as non-technical as possible... I apologize in advance if the thread is pedantic, I have no way of knowing the reader's mathematical skill level; and therefore, have assumed the lowest level as possible. I hope that to offset this, my unusual perspective on math may give some insights that are not otherwise obvious. First, I'd like to share a little background related to the topic. I am no expert, but I have done the math in my coursework, and done some tutoring. I have completed 5 courses in calculus, a couple in statistics and the tutoring of everything from basic grade school math all the way up to the 4th course in calculus. let's begin: In one-dimensional math, we have with a single horizontal number line, which has 0 in the middle and goes to infinity, incrementally, to the right and to the left. This is commonly referred to as the X axis:  This kind of number line is good for learning how to count, and add and subtract. The next time we see number lines in math, we are using two-dimensions. The same X-axis, but over the top of it, vertically is another number line, the Y-axis. Where the X and Y axes cross is called the Origin. The values for both axes where they cross is 0. This is commonly referred to as Cartesian coordinate system, where we have combinations of X and Y values to locate points that are not on the lines themselves, but in one of the four sections, called quadrants. Think: Battleship (the game), but with numbers and numbers, instead of letters and numbers. The values for X and Y are organized like this: (X,Y) as shown below.  With two-dimensions, we can go from single lines (called rays) to making two dimensional shapes and basic geometry: Triangles, Squares, Circles, et c. Three-dimensional objects such as cubes and spheres and pyramids all require a third axis, called the Z axis, where we can plot things 'in space'. Like the two dimensional cartesian graph, we need coordinates to plot points to connect together with lines; but now we add a Z-dimension: (X, Y, Z) for each point we want to plot. As shown in the sketch below, each corner of the box would have a different combination of values for X, Y and Z, with one corner of the box have all three values (0,0,0). This point is the one that is located at the origin (O). 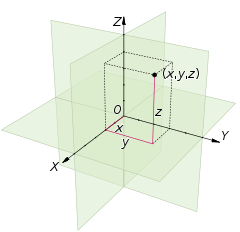 (continued) |
|
|
|
Post by yardstick on Aug 2, 2017 21:34:36 GMT -6
Continued... Okay, so we have a basic understanding of one, two and three-dimensional coordinate systems and that we can get different types of objects depending on what kind of system it is. One-dimensional objects are lines. Two dimensional objects are basic geometric shapes, like squares and circles. Three-dimensional objects are complex geometric shapes, like cubes and spheres. Would anyone like to take a guess at what a 0-dimensional object is called?While I wait for some answers I will continue by way of example for four-dimensional objects. Generally speaking, the fourth dimension is considered to be time. However, we cannot map time as a solid; and in fact, time is a property of gravity, not geometry. So, for something in the way of a geometric shape, the fourth dimension can be best exemplified by a Tesseract, which is a 4-dimensional cube. There are other shapes based off of common 3-dimensional objects which you can see if you go to the section called 'visualization' at this link: en.wikipedia.org/wiki/Regular_4-polytope#Regular_convex_4-polytopesThe Square shaped one is the Tesseract, aka a Hypercube. Incidentally, Chuck Missler pointed out that Salvador Dali had done a 4-dimensional representation of the cross/crucifixion in one of his works:  en.wikipedia.org/wiki/Crucifixion_(Corpus_Hypercubus) en.wikipedia.org/wiki/Crucifixion_(Corpus_Hypercubus)(continued) |
|
|
|
Post by yardstick on Aug 2, 2017 22:01:25 GMT -6
Continued... Okay, so we have covered one, two, three and four-dimensional objects. In physics and Engineering, we use Time as the 4th dimension, and only touch on 4-dimensional systems at the most basic level of lattices. Lattices are the atomic structures of substances like steel, or diamonds, and are represented two and three-dimensionally. However, if you looked at this link earlier en.wikipedia.org/wiki/Regular_4-polytope#Regular_convex_4-polytopesand poked around a bit, you might have seen a link called "Schlegel diagrams"; and if you clicked it, you would be starting to get into the stuff I am referring to. What we are aware of is that we have an almost impossible time representing anything beyond a three-dimensional object, because we are three-dimensional beings. Later on, I will give you a couple of overly simplistic analogies of what that is like.Now to cover 5, 6 and 7 dimensional objects we need to divert a moment. Does anyone remember imaginary numbers? We need to play around with imaginary numbers for a bit. We also might need to dabble in trigonometry and calculus a little as well. I will try to avoid them though, unless someone really wants to go there, or its absolutely necessary. Oh, and this is the point at which (after 4 dimensions) it is almost impossible to build a physical model of what we are representing mathematically, because of the 3-dimension limit of our space-time continuum. Hereafter we are going to have to cover the topics in almost pure mathematics, but we can 'simplify' a little, and i hope the simplification is digestible. (Continued) |
|
|
|
Post by watchmanjim on Aug 2, 2017 22:08:05 GMT -6
I think you already lost me. . . . .
But maybe you can explain how the tesseract represents 4 dimensions, since it looks like 3 dimensions to me.
|
|
|
|
Post by yardstick on Aug 2, 2017 22:11:08 GMT -6
I think you already lost me. . . . . But maybe you can explain how the tesseract represents 4 dimensions, since it looks like 3 dimensions to me. It is drawn in three dimensions because that is the only way we can represent it in our space-time continuum. If you go to the image on the right, below the Red 'Dali Cross' youll see a more accurate representation of a tesseract: en.wikipedia.org/wiki/TesseractIn this representation, this tesseract is 'unfolded' from a four dimensional object into a three-dimensional object: en.wikipedia.org/wiki/File:Net_of_tesseract.gifHave you ever unfolded a three dimensional cube into a flat two dimensional cross?
That is what they are doing here with a tesseract (4th dimensional cube) unfolded into a three dimensional cross.
It might help if you imagine the tesseract is made of panes of glass that can pass through each other, unlike solid objects. Thus, when the tesseract is rotated, or revolved, you see the moving pieces of the tesseract passing through each other. Here is another example, where an irregular dodecahedron (12 sided solid) is unfolded from a three dimensional object into a two dimensional object: en.wikipedia.org/wiki/Dodecahedron folded (3-D)  unfolded (2-D) Notice how the structure breaks down when one attempts to reduce the representation to a simpler dimension? Ok, I am getting a little tired right now, so I will pick this up again to discuss 5th-7th dimensional objects - which cannot be represented in our three-dimensions without severely breaking them down. (continued) |
|
|
|
Post by whatif on Aug 2, 2017 23:46:45 GMT -6
Awesome thread, yardstick! Can't wait to read more! I am the least mathematically skilled of anyone here, I'm afraid, but just looking at the amazing things you are showing us gives me a greater and greater picture of just how awesome our Creator is. Thank you so much for teaching us!
|
|
|
|
Post by watchmanjim on Aug 2, 2017 23:49:55 GMT -6
I'll compete with you for least of the mathematicians, whatif.
|
|
|
|
Post by watchmanjim on Aug 2, 2017 23:50:21 GMT -6
Now when Beloved and Brad wake up, they'll want to see this.  |
|
|
|
Post by whatif on Aug 2, 2017 23:53:49 GMT -6
Absolutely, watchmanjim! I think they'll both be really diggin' this!
|
|
|
|
Post by socalexile on Aug 3, 2017 5:10:45 GMT -6
|
|
|
|
Post by mike on Aug 3, 2017 6:07:01 GMT -6
1+1=11'teen  excellent info Yardstick...I have seen some info on line regarding Teslas 3-6-9 model of the universe. Do you know, if it ties in here somehow? |
|
Deleted
Deleted Member
Posts: 0
|
Post by Deleted on Aug 3, 2017 7:13:21 GMT -6
Would anyone like to take a guess at what a 0-dimensional object is called? A point  . Dude, this is awesome! I'm the guy who studies General Relativity in my free time, so I had to teach myself all that! I don't think it's super hard to add more dimensions to realitivity.... ever heard of Kaluza-Klien? |
|
Deleted
Deleted Member
Posts: 0
|
Post by Deleted on Aug 3, 2017 7:16:26 GMT -6
Personally, I think God is beyond dimensions; he's spirit, not flesh and bone. God is so much more than we can ever be; he transcends all limitations, except the ones He puts on Themselves. Jesus is limited by the Incarnation, but God is simply beyond dimensions, I would think.
|
|
|
|
Post by Gary on Aug 3, 2017 8:15:20 GMT -6
Wow, this thread is legit. (:
|
|
|
|
Post by kjs on Aug 3, 2017 8:18:07 GMT -6
Would anyone like to take a guess at what a 0-dimensional object is called? Technically, it would be a "point in space" However, there are some of those who argue that once a "point" becomes an object -- it ceases to be a 0-dimensional object...... Just call me Thomas; because like him I need to "SEE SOMETHING" before it begins to make sense..... I recall Dr.Missler teaching one time about there being a limit to how small something can become ..... He starts by taking a line and cutting it in half -- and points out this "Halfing" can go on and on again -- (I think the number was 10 to the-22 -- but maybe I mis-remembered) anyway once you have reduced the line to that number -- the line ceases to have locality -- or being everywhere and nowhere at once. That is when I go NO -- you are pulling my leg there ....... it cannot cease to exist....... |
|









 folded (3-D)
folded (3-D)  unfolded (2-D)
unfolded (2-D)




