|
|
Post by yardstick on Aug 6, 2017 13:22:13 GMT -6
Thanks Yardstick, that is helpful! In the unfolding hypercube, I "see" a small cube embedded within a larger cube, connected by trapezoidal planes. Each plane is a shared surface, which becomes 2 surfaces of cubes after "unfolding" into the 3-D cross. If we unfold a 3-D cube into a 2-D cross, shared edges become 2 edges.....it seems the difference in unfolding the 4-D cube in your graphic vs unfolding a 3-D cube is that the edges retain the same length when unfolding the 3-D cube, while the shape of the shared planes in the 4-D unfolding change, ie the trapezoidal planes become squares....am I completely off? Think about it this way: The way the graphic represents unfolding the hypercube is by 'stretching' the lines. But in reality, that isn't what happens. The lines really don't stretch. We are limited by our ability to represent a 4D object in 3D space again. The hypercube unfolds in exactly the same way as a regular cube does. It just does it in the 4th dimension, instead of the 3rd. When you unfold a 3D cube, you are unfolding 2D squares away from the center, right? But when you unfold a 4D hypercube, you are unfolding 3D cubes away from the center! We just cant represent that in 3D space. To do so, we either have to do as the graphic shows, and stretch the lines, distorting their shape, or pass 3D solid objects through each other! Ya can't pass a solid object through another solid object in our space-time continuum! But you can make it look that way if it is a 4D object! |
|
|
|
Post by yardstick on Aug 6, 2017 13:25:05 GMT -6
Jim, if you have a question about something you don'd understand, just send me a message and I'll do my best to create a conceptual model related to how you think. Granted there may be some times where the idea will be necessary just to memorize...
|
|
|
|
Post by whatif on Aug 6, 2017 14:30:42 GMT -6
Thanks Yardstick, that is helpful! In the unfolding hypercube, I "see" a small cube embedded within a larger cube, connected by trapezoidal planes. Each plane is a shared surface, which becomes 2 surfaces of cubes after "unfolding" into the 3-D cross. If we unfold a 3-D cube into a 2-D cross, shared edges become 2 edges.....it seems the difference in unfolding the 4-D cube in your graphic vs unfolding a 3-D cube is that the edges retain the same length when unfolding the 3-D cube, while the shape of the shared planes in the 4-D unfolding change, ie the trapezoidal planes become squares....am I completely off? The way the graphic represents unfolding the hypercube is by 'stretching' the lines. But in reality, that isn't what happens. The lines really don't stretch. We are limited by our ability to represent a 4D object in 3D space again. The hypercube unfolds in exactly the same way as a regular cube does. It just does it in the 4th dimension, instead of the 3rd. When you unfold a 3D cube, you are unfolding 2D squares away from the center, right? But when you unfold a 4D hypercube, you are unfolding 3D cubes away from the center! We just cant represent that in 3D space. To do so, we either have to do as the graphic shows, and stretch the lines, distorting their shape, or pass 3D solid objects through each other! Ya can't pass a solid object through another solid object in our space-time continuum! But you can make it look that way if it is a 4D object! Could this possibly have something to do with why Jupiter appears to sometimes step outside the boundary lines of Virgo Constellation during the pregnancy--something noted in a couple of other threads? Is it really stepping outside the lines or is it just because we are seeing it represented on the computer screen instead of in actual space? |
|
Deleted
Deleted Member
Posts: 0
|
Post by Deleted on Aug 6, 2017 15:02:11 GMT -6
Sorry if this seems convulsed; I have an answer, but it's hard to put into words!  It doesn't work that way. Virgo is defined on the celestial sphere: what the sky looks like. Since it is 2-D, we can draw lines and say that Jupiter passes it. In reality, we live in a 3-D world. The stars that look next to each other are light-years apart. In space, Jupiter doesn't pass through anything: it's when we compress all of space into a 2-D sphere around us can we say that Jupiter passes through lines. |
|
|
|
Post by whatif on Aug 6, 2017 17:12:01 GMT -6
Thank you, Beloved!
|
|
|
|
Post by yardstick on Aug 6, 2017 19:24:49 GMT -6
Sorry if this seems convulsed; I have an answer, but it's hard to put into words!  It doesn't work that way. Virgo is defined on the celestial sphere: what the sky looks like. Since it is 2-D, we can draw lines and say that Jupiter passes it. In reality, we live in a 3-D world. The stars that look next to each other are light-years apart. In space, Jupiter doesn't pass through anything: it's when we compress all of space into a 2-D sphere around us can we say that Jupiter passes through lines. Yes, although what we are really doing, rather than compressing, is projecting onto a flat surface. Like a movie. All the actors, actresses, props, et c, are 3D but you view them on a 2D plane called the movie screen. There's some nifty similarities with trying to project shadows of characters in video games, and making the shadows move relative to the characters. And with respect to the celestial sphere, God tells us in Job that Orion and Pleiades are the only two 'constellations' which actually have the stars in them gravitationally linked. That is, the stars are close by each other. All the other constellations just look like the stars are near each other, but they really aren't. If for example, you went to Alpha Centauri and looked at the constellations, ALL of them would looks different than they do from Earth. Except maybe Pleiades and Orion's belt. They might look the same, or similar. |
|
|
|
Post by yardstick on Aug 6, 2017 19:35:51 GMT -6
|
|
Deleted
Deleted Member
Posts: 0
|
Post by Deleted on Aug 6, 2017 20:24:54 GMT -6
Yardstick, I have to hand it over to you at this point, you are obviously at a higher plane of understanding on this! I wasn't concerned about stretching the lines as they unfold, as much as the trapezoidal planes at the beginning are not the same distance a to b as they are at the end....the trapezoid connecting the larger outside cube does not have the same dimension as the small cube sides after unfolding...but, it is probably a mental incapacity on my part, carry on!
|
|
|
|
Post by yardstick on Aug 6, 2017 23:08:59 GMT -6
Algebra with polynomials. ... Well, first we have to figure out which of these variables is dependent on the other. Dependent means that you have to have a value for the Independent variable before you can figure out the value of the dependent variable. Most of the time, the independent variable is x, and the dependent variable is y. There is also a special way that we represent which variable is dependent, and which variable is independent. We put the dependent variable on one side of the equals sign; and everything else, including the independent variable on the other side of the equals sign. Like this: y = x - 3 Three dimensions require x + y + z = 21, et c. All of the above examples are what is called linear systems because the exponent power of any of the variables is only 1. Linear means 'line' - the two dimensional object we previously discussed. A common template for a linear system in two dimensions is what we call the equation of a line: y = mx + b Where the value of b denotes where the line crosses the y axis if we plot the line on a graph, the value of m denotes the slope of the line. Here is an example: y = x + 9 what is the value of b? 9 what is the value of m? 1 Where do I get the 1 from? well: right? So we can re-write the equation as y = 1x + 9, showing the slope is 1 and the y-intercept (where the line crosses the y-axis if we plot it) is 9. This tells us that the value of y is going to change at the exact same rate that the value of x changes. (continued...) (Continued) Okay so we talked briefly about linear equations, which have an X and a Y - a dependent, and an independent variable. With one variable, we can plot in a one-dimensional system, with two variables a two-dimensional system, with thre variables, X, Y, Z usually, a three-dimensional system, et cetera... But before we continue, we need to cover a couple of the rules of math, namely, that rule that says if we have an equation, and we want to manipulate one side of it, we have to do the same thing to the other side. That is, what we do on one side of the equals sign, we also have to do to the other side of the equals sign. Lets take a couple of examples:  in this first example, we want to subtract 3 from the y side of the equation, so we also have to subtract 3 from the x side as well. Doing so will give us y = x - 7  in this example, we are dividing both sides of the equation by 3 to isolate the y The ultimate goal when working with these equations is to isolate the dependent variable - to get y by itself. When we do that, we can call the equation a function if it meets one criteria: when you graph it, for any point in the complete 'domain' of the equation (the line from one side of the graph to the other), a vertical line can only pass through the line of the equation once. If it does so more than once, then the equation is not a function. As a general rule, math courses don't want to over-complicate things, and so, with the exception of making the point about what is not a function, you will almost always be working with a function. So we have been talking about linear functions: y = mx + b, and we have just a couple things to cover before we move on to non-linear functions. we have been working with a function that has already been given to us, generally in the form y = mx + b. What happens if youre not given the function? What happens if you have to derive the function yourself? Well, hopefully you were given one of two options: a point with an (X,Y) coordinate, and a given slope, i.e. m= 3/4; or maybe you were given two points (X 1,Y 1) and (X 2,Y 2). Note the little numbers 1 and 2 are below the variables this time, called subscripts, so that we can tell them apart. So lets take an example of each situation. First, the slope of the line and a point known to be on the line are given to you, and you need to figure out how to do that:  in this example, we are given the coordinate point (3,1) and the slope, m = 4 Now, there is something called the 'point slope form' but honestly, this method is much easier to do. Just plug the value of m in, plug in the y part of the coordinate to y and the x part of the coordinate to x and then solve to get the only missing piece of the puzzle: b. Once you do that, you can rework the equation such that any value of X simply needs to be plugged in to get a value of Y, after writing the equation of the line that you just derived y = 4x - 1 (continued...) |
|
|
|
Post by yardstick on Aug 6, 2017 23:32:59 GMT -6
(Continued) So how about if we are only given two points? Well in order to do this, we have to first establish the slope. That is done by calulating the change in y from one point to the next, and dividing it by the change in x from one point to the next. Lets take two points : (3,2) and (5,1) and derive the equation of the line that connects the points. The first step is to calculate the slope of the line:  so the slope of the line that passes through both points is -1/2. from here we can use the same method as before, selecting one of the two points (it does not matter which one) and using it to get the value b:  So the y-intercept (where the line crosses the y-axis) is 7/2 putting it together, we get the equation of the line that passes thorough both points: y =-1/2 x + 7/2 Now, all this stuff I have been covering is really being done to get everyone to an understanding and ability to use the slope. Because it is the linchpin to most of what we are going to talk about next. Here is a link that covers slope in a little bit more depth. Also very digestible: www.coolmath.com/algebra/08-lines/04-what-is-slope-line-01(continued...) |
|
|
|
Post by yardstick on Aug 6, 2017 23:58:17 GMT -6
So when we have a linear equation/function of the form y = mx + b we can see that the slope m is constant: 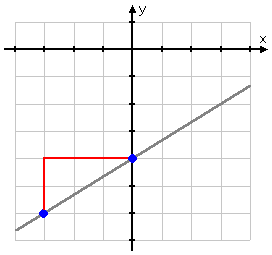 does the slope of this line ever change? or is it always constantly the same angle? Linear equations have a constant slope, m, which is equal to the change in y ---> Δy divided by the change in x ---> Δx. No matter where you are on the line, the slope is the same! What happens when you have a non-linear equation? Well, what is a non-linear equation? A non-linear equation is any equation that has an exponent in one or more of the variables that is not 1. It can be 2 or more, or it can be a fraction. (Continued...) |
|
|
|
Post by yardstick on Aug 7, 2017 20:14:35 GMT -6
(continued) Okay, so non-linear equations: the simplest one is y = x 2 which creates a parabola when you plot the X's and Y's. And this is where things start to get interesting. Remember when I asked these questions: 1. Does anyone want to take a guess as to the significance of a negative valued number equaling its reciprocal not just in size, but in location also? Because that is what I believe is occurring when we show i = -i. 2. Does anyone have a guess as to when the only time is (and its limitation) when a negative value can equal its reciprocal? Well, to answer question 1: you have two distinct points occupying the same space! This is not possible with real numbers! We might find this with electrons! And question 2: When can a negative value can equal its reciprocal? When it is an absolute value! But there's a catch! The only equal things are the magnitudes of the value! Not the position!  Whew! Okay so back to non-linear equations. Remember how the slope of the line is constant with a linear equation? Well, with non-linear equations, it isn't constant. It changes.
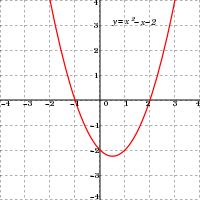 at any given point on this curve (y = x 2 - x - 2) the slope is different. Here is an example:  see how the slope changes as you move to each point? BTW, that f'(x) value you see? f' is just another way of saying the derivative... Δy Well, we cannot use m= --- for this equation, because the slope perpetually changing. It is impossible! Therefore, the m value for linear equations is considered to be the average slope, and what we Δx are looking at on this graph is the instantaneous slope. To get the instantaneous slope, we have to use calculus! But don't worry, I'll show you the easy way to do it. Let's take the simpler equation y = x 2 - x - 2 and figure out the slope. In fact, what we are going to do is figure out the formula that we can use to get the slope at any point. since Y is the dependent variable and X is the independent variable, we will do what is called taking the derivative of y with respect to x:  So what we will do is re-write the equation by following a couple of rules: 1. derivative of constants is always 0 2. to take the derivative of a variable with respect to the same variable (x to x) take the exponent, multiply the variable by it, and reduce the exponent by 1 here is an example:  The derivative of the constant, -2, is 0, the derivative of the -x is -1 and the derivative of the x 2 is 2x. Why does this work? Because dy/dx is the slope of the equation at any given point. it has the same value for non-linear equations as m does for linear equations. They are both slope! What is the slope of a horzontal, line passing through the y axis at -2? 0! what is the slope of a linear equation y = -x? --->>> y = -1x + 0 , m = -1! what is the slope of y = x 2 ? It varies linearly for any value of X you plug in -------------------->>> dy/dx = 2x: for every value of x you get 2x for the slope! its kinda like saying m = 2x! (continued...) |
|
|
|
Post by yardstick on Aug 7, 2017 21:17:14 GMT -6
(Continued) Okay, I need to skip tracks now and cover some trigonometry, because its necessary to demonstrate that 5th=10th dimension stuff. So let us begin with three basic trig functions, and something called pythagorean theorem. Pythagorean Theorem simply states that there is a relationship between all three sides of a right triangle; and that the relationship is that the sums of the squares of the non-hypotenuse sides are equal to the square of the hypotenuse. Lets look at that graphically to make it easier:  In this image, the hypotenuse of the big triangle is labeled 'a', and the two sides that we are concerned with are labeled 'b' and 'c'. Now most of the time, the sides are labeled 'a' and 'b' and the hypotenuse is labeled 'c' and so that is what we are going to use:  it doesnt matter which way you orient the triangle, the sides are a and b and the hypotenuse is c. Pythagorean Theorem is then written: a 2 + b 2 = c 2 the sum of the squares of the short sides equals the square of the hypotenuse! Next, for the three basic trig functions, we need to represent the angles, and describe them. We are going to assume that angle C in the left triangle below is 90 degrees just like the right triangle (pun not intended), even though it does not have a square to represent that. When we do, we see that there is an angle α and an angle β at the A and B vertices.   So the sine of α for the left triangle (remember we are assuming that angle C is 90 degrees) would be equal to the ratio of the side furthest away to the hypotenuse, written like this: b opposite side sine α = --- = -------------- c hypotenuse similarly the second basic trig function, cosine would be written like this: a adjacent side cosine α = --- = ------------- c hypotenuse and the last basic trig function tangent (yes it is the mathematical term for the actual thing) is written like this: b opposite side tangent α = --- = --------------- a adjacent side BTW, you will need a calculator for this. A scientific one. Your computer has one built in, but you have to turn on the scientific part of it in the options. And, these three trig functions plus pythagorean theorem are things ya gotta memorize, as far as I know, there is no way to derive them. (continued...) |
|
|
|
Post by yardstick on Aug 9, 2017 21:22:44 GMT -6
Okay, so this has likely gotten a bit tedious for everyone, so it would probably be easier to have anyone interested just send a message...
|
|
|
|
Post by whatif on Aug 9, 2017 22:31:58 GMT -6
I'm not finding it tedious at all, yardstick! I love looking at the graphics you've provided!
|
|